Rappresentazione dei numeri complessi

Nella pagina "Numeri complessi e campo complesso" è stato introdotto il campo complesso descrivendone gli elementi, le operazioni e le proprietà. In questa pagina ci si concentra su come gli elementi di ℂ, i numeri complessi, possono essere algebricamente rappresentati.  

Il campo complesso è un insieme di numeri, detti appunto numeri complessi, definito come:

ℂ  ≔ {(x,y) | x,y ∈ ℝ}

cioè l’insieme delle coppie ordinate (x,y) con x, y numeri reali. In particolare è definito con i ≔ (0,1) l’unità immaginaria che distingue il campo complesso dal campo reale. Quest’ultimo può essere inoltre ridefinito come segue:

ℂ ⊇ ℝ ≔ {(x,0) | x ∈ ℝ}

In ℂ sono definite le seguenti operazioni di somma e prodotto:

(a,b) + (c,d) = (a+c,b+d)

(a,b)(c,d) = (ac-bd,bc+ad)

Sia quindi dato un generico numero complesso z = (x,y) nel piano di Gauss. 

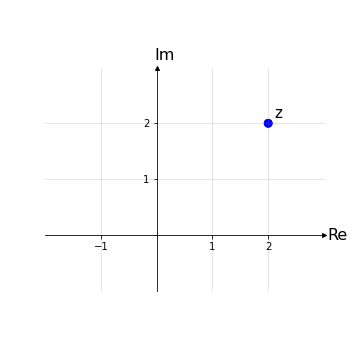
Rappresentazione cartesiana dei numeri complessi

Usando le definizioni delle operazioni di somma e prodotto e quella di unità immaginaria, segue che:

(x,y) = (x,0) + (0,y) = x + (0,y) = x + (0,1)(y,0) = x + (0,1)y = x + iy

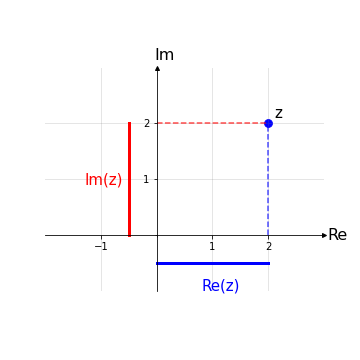
Quindi un generico elemento z ∈ ℂ, z = (x,y) può essere scritto anche come z = x + iy, con x, y ∈ ℝ. In particolare, il numero 'x' viene detto parte reale di z, mentre il numero 'y' parte immaginaria di z:

z = x + iy

Re(z) ≔ x Im(z) ≔ y

\(z = Re(z) + i \cdot Im(z)\)

Questa è detta rappresentazione cartesiana di un numero complesso che nel piano di Gauss viene graficata come segue:

Esempio 1: Siano z₁ = 2 + 1i, z₂ = -1 + 3i, z₃ = - 3i. Si rappresentino tali numeri complessi nel diagramma di Gauss.

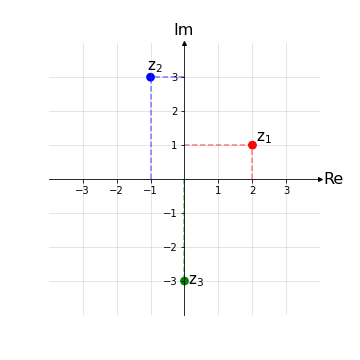
Nota: La rappresentazione cartesiana permette di svolgere facilmente operazioni di somma e complesso coniugato. Tuttavia si rivela parecchio complicata nelle operazione di prodotto, elevamento a potenza, radice n-esima.

Esempio 2: Si calcoli somma e differenza di z₁ = 2 + 1i, z₂ = -1 + 3i e il complesso coniugato di entrambi.

z₁+z₂ = 2+(-1) + i(1+3) = 1 +4i

z₁-z₂ = 2-(-1) + i(1-3) = 3 - 2i

\(\overline{z_1} = 2 - 1i\) 

\(\overline{z_2} = -1 - 3i\) 

Rappresentazione trigonometrica dei numeri complessi

Un altro modo per individuare univocamente i numeri complessi è quello di usare le coordinate polari per rappresentarli in forma trigonometrica.

Sia dato il numero complesso z espresso in forma cartesiana come z = x + iy.

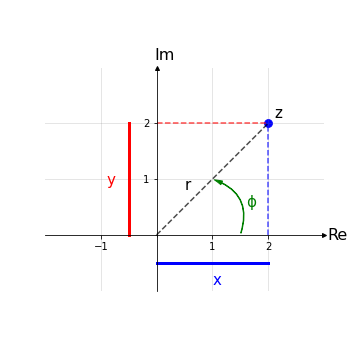
Nel grafico sopra le coordinate (r,Φ) sono le coordinate polari e, come si vede, possono essere usate in alternativa alle coordinate (x,y) per identificare lo stesso numero z nel piano di Gauss. A differenza delle coordinate cartesiane, dove x,y ∈ (-∞,+∞), per le coordinate polari dobbiamo imporre come dominio delle coordinate:

 r ∈ [0,+∞)

Φ ∈ [0,2𝜋) oppure Φ ∈ (-𝜋,𝜋]

con r detto modulo e Φ detto argomento di z, angolo che il segmento r forma con il semiasse positivo delle ascisse; in particolare il modulo fissa una circonferenza di raggio r e la coordinata angolare scorre su di essa individuando il numero z in questione.

Utilizzando le formule trigonometriche per un triangolo rettangolo si ottiene il legame tra (x,y) e (r,Φ):

\(\left\{\begin{array}{@{}l@{}l} x = r \cdot cos\phi\\  y = r \cdot sin\phi \end{array}\right.\, \)

Il numero complesso z = x + iy può essere quindi riscritto in forma trigonometrica come:

\( z = r cos\phi + ir sin\phi = r(cos\phi + i sin\phi) \)

Esempio 3: Si rappresentino i seguenti numeri complessi nel diagramma di Gauss:

\( z_1 = \sqrt{5} ( cos(arctan\frac{1}{2}) + i sin(arctan\frac{1}{2}) ) \)

\( z_2 = \sqrt{10} ( cos(arctan3) + i sin(arctan3) ) \)

\( z_3 = 3 ( cos\frac{3\pi}{2} + i sin\frac{3\pi}{2} ) \)

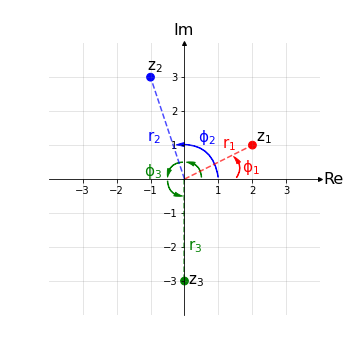
Nota: La rappresentazione trigonometrica permette di svolgere facilmente operazioni di prodotto, complesso coniugato, elevamento a potenza, radice n-esima. Tuttavia si rivela parecchio complicata nell'operazione di somma e, in alcuni casi, nella rappresentazione grafica sul piano di Gauss.

Esempio 4:  Si calcolino prodotto e rapporto tra z₁, z₂ e il complesso coniugato di z₁ con 

\( z_1 = r_1 (cos\phi_1 + i sin\phi_1) \)

\( z_2 = r_2 (cos\phi_2 + i sin\phi_2) \)

\(z_1 \cdot z_2 = r_1 r_2 (cos(\phi_1+\phi_2) + i sin(\phi_1+\phi_2))\)

\(\frac{z_1}{z_2} = \frac{r_1}{r_2} (cos(\phi_1-\phi_2) + i sin(\phi_1-\phi_2))\)

\(\overline{z_1} = r_1 (cos(\phi_1) - i sin(\phi_1))\)

Per approfondire meglio il legame tra coordinate polari e cartesiani si consiglia di consultare la pagina “Cambio di coordinate per la rappresentazione dei numeri complessi”.

Rappresentazione esponenziale dei numeri complessi

Un terzo modo per rappresentare algebricamente un numero complesso è quello di ricorrere alla formula di Eulero:

\(e^{i\phi} = cos\phi + i sin\phi \)

Quindi preso un numero complesso z espresso in forma trigonometrica come:

\( z = r(cos\phi + i sin\phi) \)

usando la formula sopra possiamo riscriverlo come:

\( z = re^{i\phi} \)

detta forma esponenziale di un numero complesso. (r,Φ) sono le solite coordinate polari definite sempre nei domini  r ∈ [0,+∞) e Φ ∈ [0,2𝜋) oppure Φ ∈ (-𝜋,𝜋].

Nota: In termini di rappresentazione nel piano di Argand-Gauss non ci sono differenze in quanto si utilizzano sempre le coordinate polari.

Esempio 5: Si rappresentino i seguenti numeri complessi nel diagramma di Gauss:

\( z_1 = 2 e^{i\frac{3\pi}{2}} \)

\( z_2 = \sqrt{2} e^{i\pi} \)

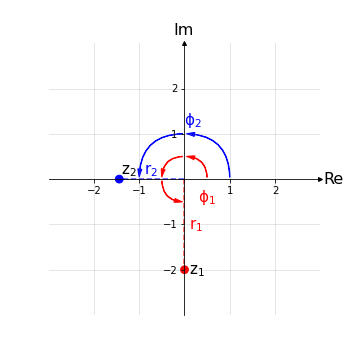
Nota: La rappresentazione esponenziale permette di svolgere facilmente operazioni di prodotto, complesso coniugato, elevamento a potenza, radice n-esima. Tuttavia si rivela parecchio complicata nell'operazione di somma e, in alcuni casi, nella rappresentazione grafica sul piano di Gauss.

Esempio 6:  Si calcolino prodotto e rapporto tra z₁, z₂, il complesso coniugato di z₁ e la potenza n-esima di z₂ con:

\( z_1 = r_1 e^{i\phi_1} \)

\( z_2 = r_2 e^{i\phi_2} \)

\(z_1 z_2 = r_1 r_2 e^{i(\phi_1 + \phi_2)}\)

\(\frac{z_1}{z_2} = \frac{r_1}{r_2} e^{i(\phi_1 - \phi_2)}\)

\(\overline{z_1} = r_1 e^{i(-\phi_1)}\) 

\({z_2}^{n} = {r_2}^{n} e^{in\phi_2}\)