Piano di Argand-Gauss
In riferimento alla precedente pagina "Numeri complessi e campo complesso" si mostra come rappresentare graficamente il campo complesso, i suoi elementi e alcune operazioni che si possono svolgere su di essi.
Ricordando la definizione del campo complesso ℂ:
ℂ ≔ {z ∈ ℂ | z = (x,y) con x,y ∈ ℝ}
cioè è l’insieme delle coppie ordinate (x,y) con x, y numeri reali. Come già visto, questa definizione si può ricondurre all’operazione di prodotto cartesiano tra insiemi: l’insieme dei numeri complessi è in corrispondenza biunivoca con il prodotto cartesiano di ℝ con sé stesso.
ℂ ≔ ℝ x ℝ oppure ℂ ≔ ℝ2
Per rappresentare i numeri complessi sfruttiamo quindi questa corrispondenza e grafichiamo il cosiddetto piano di Argand-Gauss:
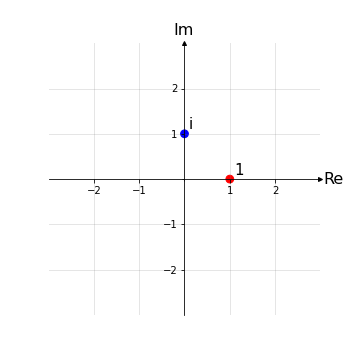
Per molti aspetti ricorda il classico piano cartesiano che viene sempre usato per rappresentare funzioni reali in una variabile: ogni punto/elemento è univocamente individuato da una coppia di coordinate del tipo (x,y). Tuttavia è presente una differenza sostanziale: nel piano cartesiano gli assi x e y sono entrambi assi reali, invece nel piano di Argand-Gauss solo l’asse orizzontale è l’asse reale (Re), mentre l’asse verticale è detto asse immaginario (Im). In sintesi:
lungo l’asse reale (Re) si incontrano numeri reali: -1, 0, 1, 2, …
lungo l’asse immaginario (Im) si incontrano numeri immaginari puri: -1i, 0i, 1i, 2i, …
Nel diagramma sopra sono stati evidenziate l’unità reale (1,0), corrispondente al numero 1, e l’unità immaginaria (0,1), corrispondente al numero i.
Numeri complessi nel piano di Argand-Gauss con coordinate cartesiane
Sia z ∈ ℂ, z = (x,y). Come visto nella precedente pagina introduttiva il numero complesso z può anche essere espresso come:
z = x + iy
detta rappresentazione cartesiana di un numero complesso.
Coerentemente con il piano di Argand-Gauss, il numero x viene detto parte reale di z, mentre il numero y parte immaginaria di z.
Re(z) ≔ x Im(z) ≔ y
z = Re(z) + i*Im(z)
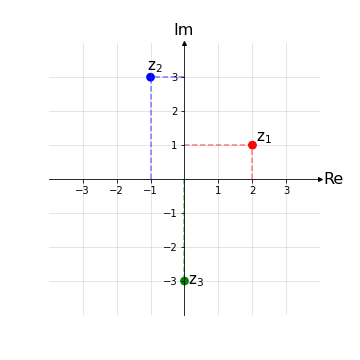
Esempio 1: Siano z1 = 2 + 1i, z2 = -1 + 3i, z3 = - 3i. Si rappresentino tali numeri complessi nel diagramma di Argand-Gauss.
Tutto quello che c’è da fare è individuare Re(zi) e Im(zi), riportare tali valori sui rispettivi assi e trovare il punto i-esimo zi prolungando una retta perpendicolare ad ogni asse fino alla loro intersezione. In particolare si noti che Re(z3) = 0, quindi tale punto si troverà proprio sull’asse immaginario.
Numeri complessi nel piano di Argand-Gauss con coordinate polari
Un altro modo per individuare univocamente i numeri complessi è quello di usare la loro forma trigonometrica e le coordinate polari. Qua ci si limita a fornire sommariamente le relazioni tra le coordinate senza ulteriori giustificazioni: per ulteriori approfondimenti si legga "Rappresentazione dei numeri complessi".
Sia z = x + iy. Tale numero complesso può anche essere espresso come:
z = rcosΦ + irsinΦ = r(cosΦ + isinΦ)
\(\left\{\begin{array}{@{}l@{}l} x = r cos\phi\\ y = r sin\phi \end{array}\right.\, \)
con r ∈ [0,+∞) e Φ ∈ [0,2𝜋)
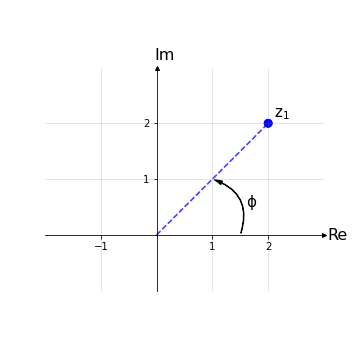
Con r detto modulo e Φ detto argomento di z; in particolare il modulo fissa una circonferenza di raggio r e la coordinata angolare scorre su di essa individuando il punto z in questione. Graficamente tutto ciò si traduce come segue:
Operazioni nel piano di Argand-Gauss in coordinate cartesiane
Per sintesi si trattano alcuni esempi semplici in coordinate cartesiane ma un discorso simile può anche essere fatto in coordinate polari con gli opportuni accorgimenti.
A differenza del campo reale ℝ, in campo complesso ℂ sono definite le seguenti operazioni di somma e prodotto, che proviamo a graficare:
(a,b) + (c,d) = (a+c,b+d)
(a,b)(c,d) = (ac-bd,bc+ad)
Esempio 2: Siano z1 = 2 + 1i, z2 = -1 + 3i. Si rappresenti la somma e il prodotto di tali numeri complessi nel diagramma di Argand-Gauss.
Applicando le definizioni z1+z2= 1+4i e \( z_1\cdot z_2 \) = -5+5i.
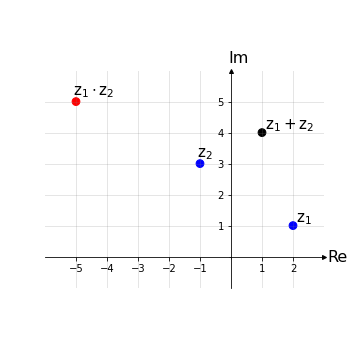
Nota: L’operazione di prodotto tra numeri complessi non è così intuitiva, soprattutto in coordinate cartesiane, proprio perché definita diversamente dal solito prodotto in campo reale a cui si è abituati. Per avere un’idea più chiara di come avviene tale operazione è necessario passare alla rappresentazione esponenziale dei numeri complessi.
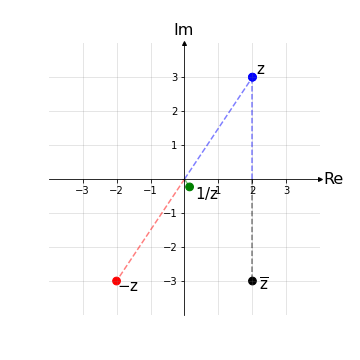
Sia dato un numero z = x+iy. Rappresentiamo ora nel piano di Argand-Gauss i seguenti elementi relativi al numero z generico:
l’opposto di z è (-x,-y), cioè il simmetrico rispetto all’origine
l’inverso di z è \(\left(\frac{x}{\sqrt{(x^2+y^2)}},\frac{-y}{\sqrt{(x^2+y^2)}}\right)\)
il complesso coniugato di z è \(\overline{z}\) ≔ (x,-y), cioè il simmetrico rispetto all’asse reale