Prodotto cartesiano di due insiemi

Dati due insiemi non vuoti A e B, l’insieme di tutte le coppie ordinate ottenute a partire dagli elementi di A e di B viene detto prodotto cartesiano di A per B (o di B per A):A × B ≔ {(a,b) | a ∈ A, b ∈ B}   oppure   B × A ≔ {(b,a) | a ∈ A, b ∈ B} con A × B ≠ B × A in generale sempre per la condizioni di ordine, ossia l’operatore × di prodotto cartesiano tra due insiemi non è commutativo.

NOTA: date tutte le coppie ordinate creabili dagli elementi di un insieme A si può utilizzare la seguente notazione: A × A = A², ovvero il caso A = B.

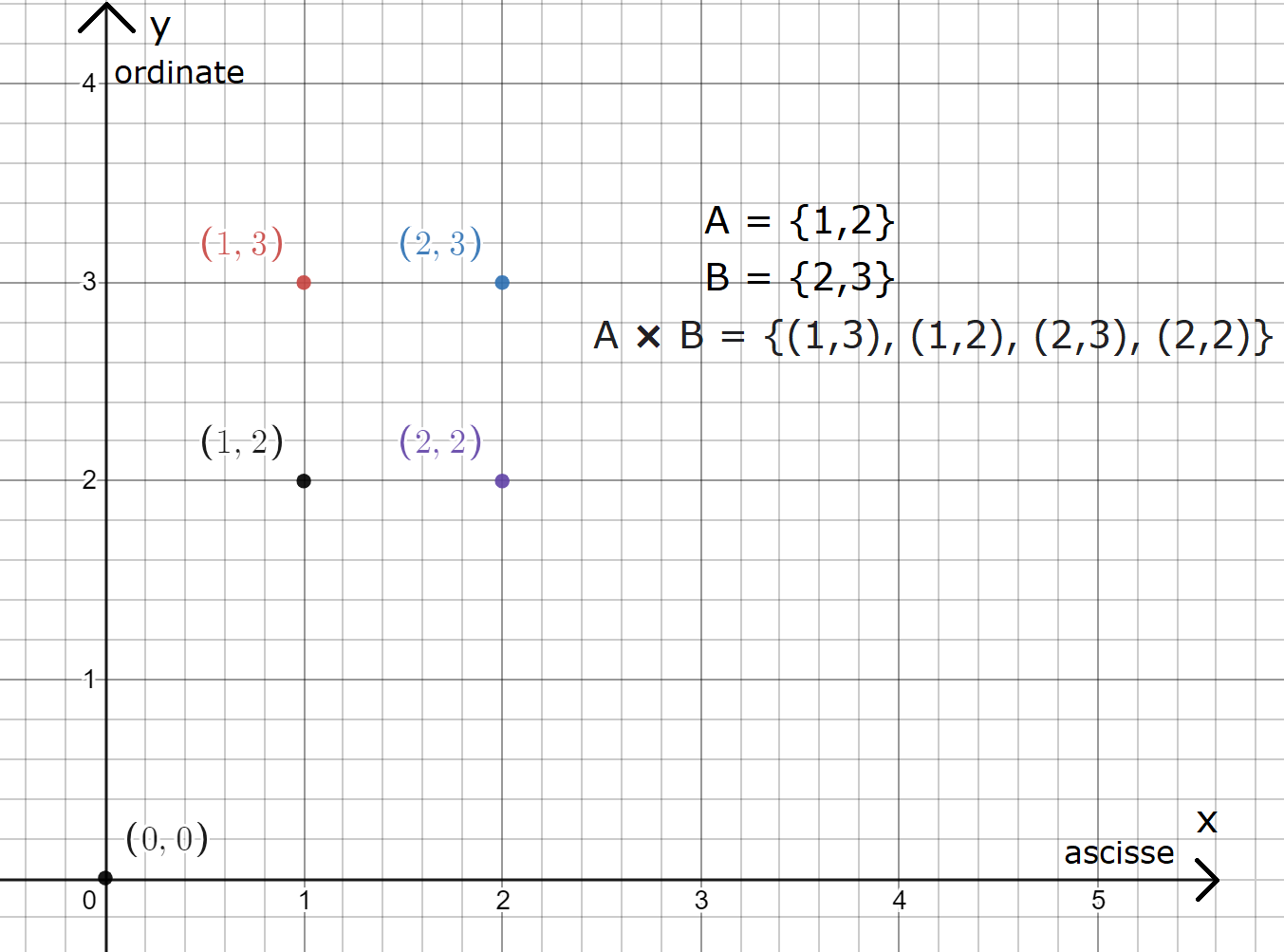
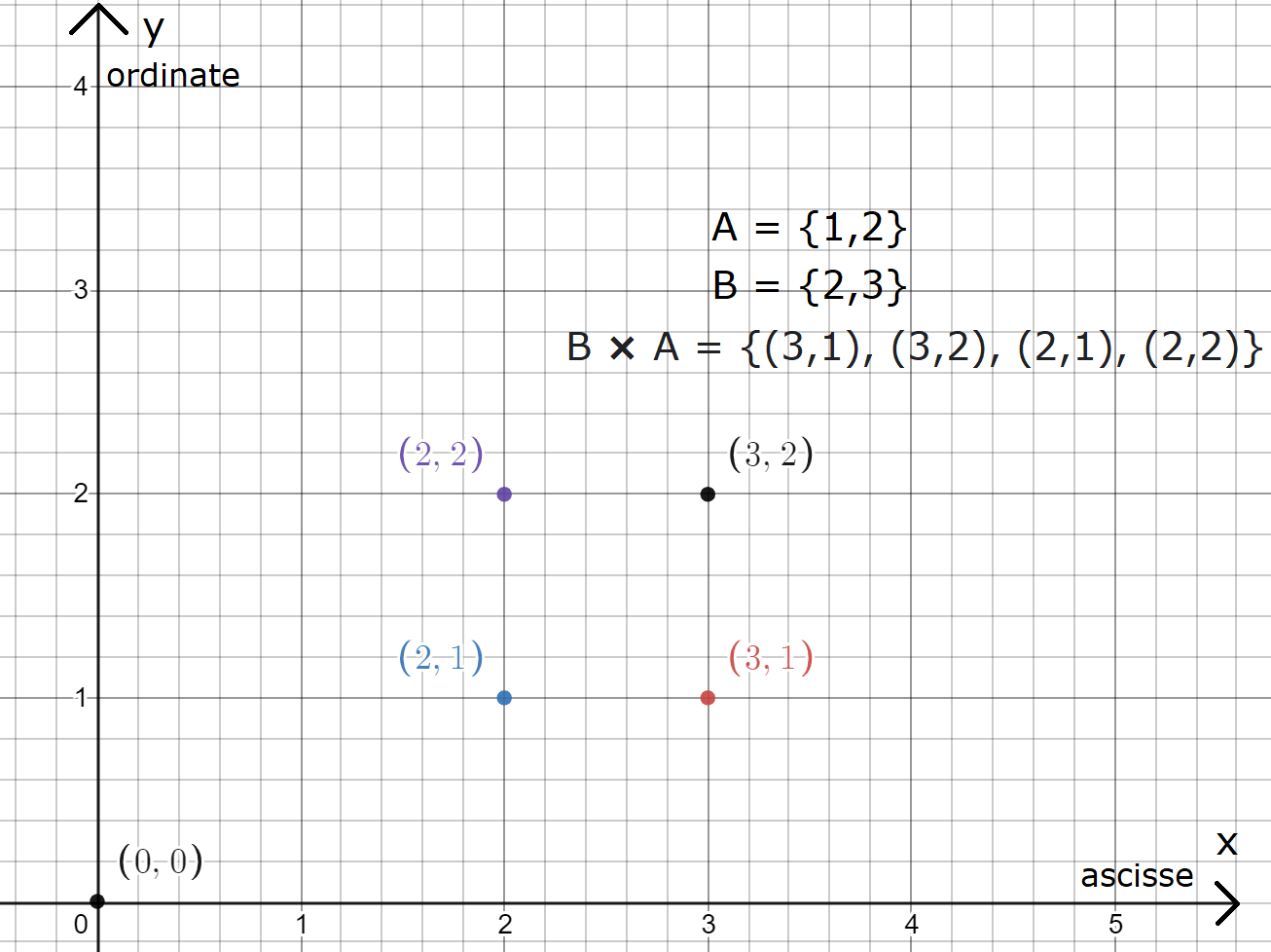
Esempio 1: siano dati i due insiemi A = {1,2}, B = {3,2} tra i quali attuiamo l’operazione di prodotto cartesiano ottenendo i due seguenti insiemi in base all’ordine di applicazione:A × B = {(1,3), (1,2), (2,3), (2,2)}B × A = {(3,1), (3,2), (2,1), (2,2)}

Esempio 2: siano dati gli insiemi A = ∅ e B = {1, 2, 3} e applichiamo il prodotto cartesiano:A × B = ∅    B × A = ∅ La spiegazione di questo risultato è dovuta al fatto che uno dei due insieme non contiene elementi e non è quindi possibile costruire alcuna coppia: si noti infatti nella definizione come sia stata posta l’ipotesi di insiemi non vuoti.

Rappresentazione grafica del prodotto cartesiano

Uno strumento grafico utile (ma non l’unico) per visualizzare l’operazione di prodotto cartesiano tra due insiemi è quello di rappresentare le coppie ordinate (a,b) nel piano cartesiano.

Il piano cartesiano è un sistema di riferimento in cui, fissata un’unità di misura, ogni punto viene individuato da una coppia ordinata le cui componenti sono dette coordinate cartesiane. Esso consiste in due rette orientate ortogonali tra loro, una orizzontale detta ascissa e una verticale detta ordinata, con origine il punto O di intersezione tra le due; tale origine è indicata dalla coppia (0,0).

Per convenzione poniamo come ascissa gli elementi x ∈ X e come ordinata gli elementi y ∈ Y. In generale X e Y coincidono con l’insieme dei numeri reali ℝ e ogni punto del piano rappresenta quindi un elemento del prodotto cartesiano di X × Y, che equivale all’insieme ℝ².

Riprendendo l’esempio 1 del paragrafo precedente proviamo a rappresentare i suoi elementi nel piano cartesiano prestando attenzione al porre in ascissa il primo termine dell’operazione di prodotto cartesiano. Fissiamo come unità di riferimento 1, ossia ogni tacca lungo gli assi del piano rappresenta un salto di 1; il risultato che otteniamo è il seguente:

Il prodotto cartesiano è caratterizzato, in particolare, dalla proprietà distributiva rispetto alle operazioni di unione, intersezione, differenza e complementazione. Per una trattazione più dettagliata rimandiamo alla pagina dedicata alle proprietà del prodotto cartesiano.

NOTA: Il concetto di prodotto cartesiano può essere esteso ad un caso più generale di n-uple ordinate (a₁,a₂,...,a_n) come elementi dell’insieme A₁ × A₂ × … × A_n con a_i ∈ A_i con i = 1, 2, ..., n.
Per tali n-uple valgono ancora tutte le proprietà elencate nella pagina dedicata.