Rappresentazione delle radici complesse nel piano di Gauss

Nella pagina "Radici n-esime di un numero complesso" è stata spiegata un’altra importante differenza tra campo reale e campo complesso per quanto riguarda l’operazione di radice n-esima, n ∈ ℕ⁺. In questa pagina si amplia l’argomento introducendo un’interpretazione geometrica delle radici.

Si è mostrato come, dalla rappresentazione trigonometrica e dalla formula di De Moivre, le radici n-esime di un numero complesso possono essere facilmente calcolate usando la seguente formula:

\(z^{\frac{1}{n}} = r^{\frac{1}{n}} \left[cos\left(\frac{\phi}{n}+\frac{2\pi k}{n}\right) + i sin\left(\frac{\phi}{n}+\frac{2\pi k} {n}\right)\right]\) con n ∈ ℕ⁺, k ∈ ℤ

In particolare è stato sottolineato come, al variare di k, si ottengono tutte le n-esime radici complesse di z, con periodicità dopo n valori di k: per comodità conviene quindi prendere i valori k = 0, 1, …, n-1. Dalla formula si può notare che ad ogni unità di incremento di k corrisponde una aggiunta di un fattore \(2\pi/n\):

\begin{align*} \sqrt[n]{z} &\stackrel{\rm k=0}{=} \sqrt[n]{r} \left[cos\left(\frac{\phi}{n}\right) + i sin\left(\frac{\phi}{n}\right)\right];\\  \sqrt[n]{z} &\stackrel{\rm k=1}{=} \sqrt[n]{r} \left[cos\left(\frac{\phi}{n}+\frac{2\pi}{n}\right) + i sin\left(\frac{\phi}{n}+\frac{2\pi}{n}\right)\right]. \\  \vdots \end{align*}

e così via per ogni incremento da k=j a k=j+1, con j indice intero arbitrario.

Interpretazione geometrica

Sia dato un numero complesso z, \((r,\phi)\) e le sue n-radici calcolate con l’equazione sopra. Dalla forma trigonometrica, e quindi dalle coordinate polari, delle radici si può dedurre che esse si trovano su una circonferenza nel piano di Gauss di raggio \(\sqrt[n]{r}\), con centro banalmente nell’origine (0,0) per come sono state definite le coordinate polari. L’angolo della prima radice (k=0) è pari a \(\phi/n\) e, come visto nel paragrafo precedente, ad ogni incremento unitario di k, viene aggiunto un angolo \(2\pi/n\).

Nota: Rispetto alla radice con angolo dato da k=0, la radice con angolo dato da k=n risulta avere un incremento di angolo pari a  \(2n\pi/n = 2\pi\): l’angolo è trigonometricamente uguale per i casi k=0 e k=n e corrisponde a \(\phi/n\).

Riassumendo ogni radice \(w_k\) avrà le seguenti coordinate polari: 

\(\begin{cases}  r_k = \sqrt[n]{r} \\ \varphi_{k} = \frac{\phi}{n} + \frac{2k\pi}{n}\end{cases}\)

dove \((r,\phi)\) sono le coordinate del numero complesso z a cui è stata applicata l’operazione di radice n-esima. Il risultato è un poligono regolare di n lati inscritto nella circonferenza di raggio \(r_k\) non degenere per n ≥ 3. 

Esempi rappresentazione radici complesse

Vengono ripresi i due esercizi risolti nella pagina "Radici n-esime di un numero complesso" per mostrarne il risultato geometrico.

Esempio 1: Si calcolino le radici quadrate del numero z = i.

(...) Le radici \(w_k\) trovate sono le seguenti:

\begin{align*} w_0 &= cos\left(\frac{\pi}{4}\right) + i sin\left(\frac{\pi}{4}\right);\\ w_1 &= cos\left(\frac{5\pi}{4}\right) + i sin\left(\frac{5\pi}{4}\right);\\ \end{align*}

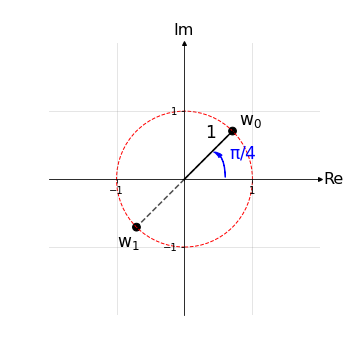
Come ci si aspetta le radici quadrate sono soltanto due, indipendentemente dal valore di k, e sono simmetriche rispetto all’origine delle coordinate (0,0): per le radici quadrate, infatti, n=2 e il fattore angolare diventa \(2\pi/2 = \pi\), cioè mezzo giro.

Esempio 2: Si calcolino le radici quarte del numero z = 1+i.

(...) Svolgendo tutti i calcoli le radici \(w_k\) risultano:

\begin{align*} w_0 &= \sqrt[4]{2} \left[cos\left(\frac{\pi}{16}\right) + i sin\left(\frac{\pi}{16}\right)\right];\\ w_1 &= \sqrt[4]{2} \left[cos\left(\frac{9\pi}{16}\right) + i sin\left(\frac{9\pi}{16}\right)\right];\\ w_2 &= \sqrt[4]{2} \left[cos\left(\frac{17\pi}{16}\right) + i sin\left(\frac{17\pi}{16}\right)\right];\\ w_3 &= \sqrt[4]{2} \left[cos\left(\frac{25\pi}{16}\right)  + i sin\left(\frac{25\pi}{16}\right)\right].\\ \end{align*}

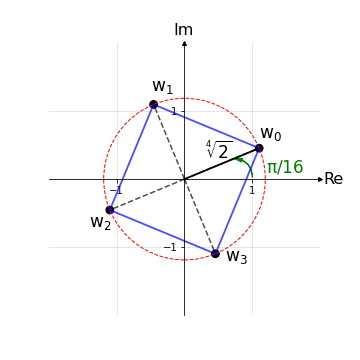
Come ci si aspetta le radici quarte sono esattamente quattro, indipendentemente dal valore di k, e formano un poligono regolare di quattro lati (quadrato): per le radici quarte, infatti, n=4 e il fattore angolare diventa \(2\pi/4 = \pi/2\), cioè un quarto di giro.