Relazioni binarie e loro grafici

Si consiglia di avere ben chiari i concetti di coppia ordinata (x,y) e la definizione di prodotto cartesiano spiegati alle pagine indicate.

Riassumendo brevemente si ricordi come, in generale, (x,y) ≠ (y,x) ovvero in una coppia ordinata l’ordine è fondamentale. Dati due insiemi possiamo definire il prodotto cartesiano come l’insieme di tutte le coppie ordinate costruibili con gli elementi dei due insiemi, rispettando sempre la condizione di ordinamento: tale condizione è il motivo per cui l’operazione di prodotto cartesiano non è commutativa.

Dati due insiemi non vuoti A e B si definisce una relazione binaria r tra gli elementi a ∈ A e gli elementi b ∈ B un predicato binario r(a,b) nelle suddette variabili; a e b sono in relazione tra loro solo se r predicato è vero.

Sia inoltre ℜ ⊆ A x B, sottoinsieme del prodotto cartesiano, definito come segue:

ℜ ≔ {(a,b) | (a,b) ∈ A × B ⋀ r(a,b)}

ovvero tutte le coppie dell’insieme prodotto cartesiano di A per B per cui la relazione r risulta vera. ℜ viene detto grafico della relazione r e quindi, per indicare che due elementi a e b sono legati da r, si scrive (a,b) ∈ ℜ.

Viceversa dato ℜ ⊆ A × B risulta individuabile una r tale che r(a.b) ⇔ (a,b) ∈ ℜ: ovvero la relazione è verificata nella coppia in considerazione solo se tale coppia appartiene al grafico della relazione..

Nota: Se A = B si avrà che r è una relazione tra gli elementi di uno stesso insieme, A o B che sia.

Siano dati due insiemi non vuoti A,B e una relazione r(a,b) con a ∈ A, b ∈ B.

L’insieme A è detto dominio della relazione mentre l’insieme B è il codominio della relazione.

Il sottoinsieme di B i cui elementi soddisfano r viene detto immagine della relazione mentre il sottoinsieme di A i cui elementi soddisfano r viene denominato controimmagine della relazione.

Banalmente quindi l’immagine sarà per forza contenuta nel codominio mentre la controimmagine sarà contenuta nel dominio; nulla vieta che questi insiemi possano coincidere.

Esempi di relazioni binarie

Esempio 1: Nel nostro linguaggio una relazione binaria può essere "x è figlio di y" oppure "x ha meno anni di y".

Esempio 2: Nell’ambito matematico invece un esempio può essere, dato X ≔ "insieme dei numeri naturali > 0", la relazione r(a,b) tale che "a e b siano primi tra loro" ⋀ a, b ∈ X .

Per fare un paio di esempi concreti prendiamo gli insiemi A ≔ {1,2,3} e B ≔ {1,2,3,4}.

Esempio 3: Data una relazione r qualsiasi e dati i seguenti due grafici ℜ possiamo, usando la definizione stessa di ℜ, capire se tali grafici sono o meno accettabili.

ℜ₁ ≔ { (1,1), (2,2), (3,3), (4,4) }

ℜ₂ ≔ { (1,2), (1,3), (1,4), (2,3),  (2,4), (3,4) }

Il primo grafico non è accettabile in quanto per la coppia (4,4) non abbiamo tutti gli elementi negli insiemi di partenza A e B: in questo caso 4 ∉ A. Sostanzialmente ℜ₁ non è sottoinsieme di A x B.

Il secondo grafico è invece accettabile in quanto tutti i suoi elementi appartengono al prodotto cartesiano di A x B. In particolare una possibile relazione di ℜ₂ può essere definita come r(a,b) ≔ "a strettamente minore di b".

Esempio 4: Considerando gli insiemi A, B precedenti e data la relazione r(a,b) ≔ "a + b = 5" scriviamo il grafico ℜ₃ di tale relazione:

ℜ₃ ≔ { (1,4), (2,3), (3,2) }

Volendo esercitare un attimo il lessico, diremo che A è il dominio di r e gli elementi di A che compaiono nelle coppie di ℜ₃ sono la controimmagine di r: {1,2,3} che in questo caso coincide proprio con A. Concludendo possiamo dire che B è il codominio di r e gli elementi di B che compaiono nelle coppie di ℜ₃ sono oggetti appartenenti all’immagine di r: {2,3,4} che in questo caso non coincide con B.

Esempio 5: Altri esempi, con cui si avrà a che fare più di frequente, possono essere, dati X = Y, X ≔ ℝ con r₁ ≔ "x ≤  y" oppure r₂ ≔ "x²+y² = 1" per le quali disegniamo i rispettivi grafici: 

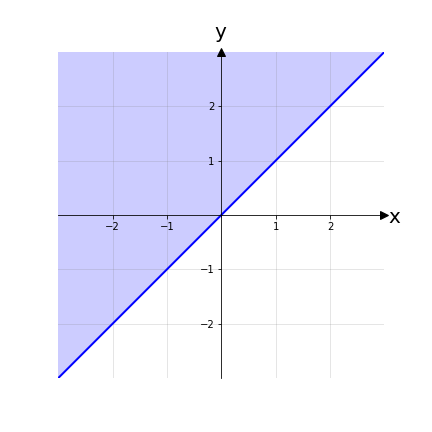
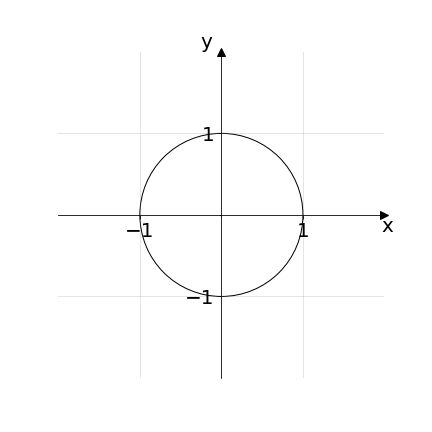
Nota: La relazione r₂ è proprio quella che descrive una circonferenza di raggio 1 centrata nell’origine del piano cartesiano.

Tra tutte le relazioni risaltano per importanza nell’analisi, e non solo, le equivalenze e gli ordinamenti.