Il limite di una funzione: definizione ed esempi

Il concetto di limite è fondamentale in matematica, specialmente nell'ambito dell'analisi matematica. Esso descrive il comportamento di una funzione quando l'input si avvicina nell’intorno di un certo valore, senza necessariamente raggiungerlo. I limiti sono essenziali per la comprensione di concetti avanzati come la derivata e l'integrale, e sono applicati in vari campi della scienza e dell'ingegneria.

Che cos'è un limite?

In termini semplici, il limite di una funzione in un punto descrive il valore al quale si avvicina la funzione quando l'input si avvicina all’intorno di quel punto. Tuttavia, è cruciale notare che il limite non è necessariamente il valore della funzione in quel punto, se esiste.

Matematicamente, il limite di una funzione f(x) mentre x tende a un valore a è denotato come:

\(\lim_{x\to x_0} f(x)\)

Questo simbolismo non descrive il valore di f(x) quando x è esattamente uguale ad \(x_0\), ma piuttosto il valore al quale f(x) si avvicina mentre x si avvicina ad \(x_0\), ovvero nell’intorno di \(x_0\).

Il limite di una funzione per un certo punto, può essere analizzato in diverse maniere:

• I limiti laterali: questi descrivono il comportamento di una funzione mentre l'input si avvicina a un valore da sinistra (denotato con \(\lim_{x\to x_0^-} f(x)\)) o da destra (denotato con \(\lim_{x\to x_0^+} f(x)\)).

• Limiti all'Infinito: analizzano il comportamento di una funzione mentre l'input cresce senza limiti (denotato come \(\lim_{x\to +\infty} f(x)\)) o decresce senza limiti (denotato come \(\lim_{x\to -\infty} f(x)\)).

Distinguiamo tra quattro tipi di limiti:

1. Il limite finito di una funzione per x che tende ad un valore finito

2. Il limite finito di una funzione per x che tende all’infinito

3. Il limite infinito di una funzione per x che tende ad un valore finito

4. Il limite infinito di una funzione per x che tende ad un valore infinito

Due esempi per capire il concetto di limite

Consideriamo la seguente funzione:

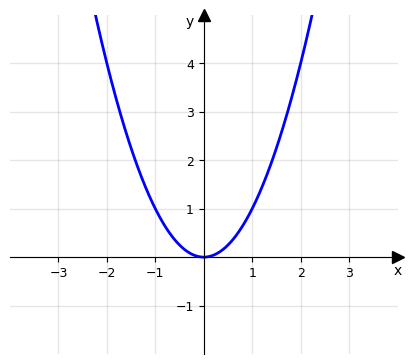
\(y=f(x)=x^2\)

e studiamo il comportamento della funzione quando x assume valore prossimi allo 0.

Possiamo osservare che quando la variabile x assume valori più vicini allo 0, anche la variabile y si avvicina sempre di più allo 0. Infatti scriveremo che:

\(\lim_{x\to 0}x^2=0\)

Possiamo confermare questo comportamento anche osservando graficamente la funzione.

Per il secondo esempio, invece, consideriamo la seguente funzione:

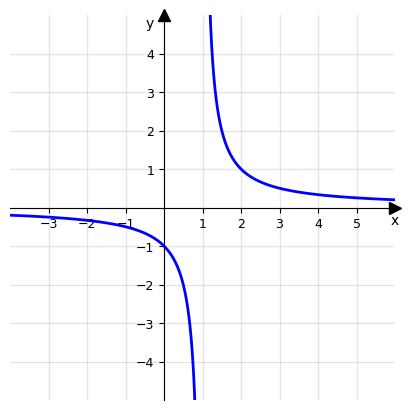
\(y=f(x)=\frac{1}{x-1}\)

e analizziamo come la funzione si comporta quando x assume valori prossimi a 1.

Quello che possiamo notare è che man mano che la variabile x si avvicina al valore 1, il valore della variabile y diventa sempre più grande o più piccolo, in base al lato da cui ci avviciniamo. In particolare abbiamo che il:

\(\lim_{x\to 1^-}f(x) = -\infty\) e \(\lim_{x\to 1^+}f(x) = +\infty\)

Questo si tratta di un esempio particolare in cui il comportamento della funzione nell’intorno del punto cambia in base al lato. Questo significa che il comportamento della funzione in un intorno sinistro di x_0, è diverso dal comportamento in un intorno destro di x_0.

Questo comportamento si può osservare anche tramite una interpretazione grafica della funzione considerata.

Come calcolare i limiti

Il calcolo dei limiti può variare da semplice a estremamente complesso. In alcuni casi, è possibile sostituire direttamente il valore di x nella funzione. In altri casi, sono necessarie tecniche più sofisticate, come la semplificazione della funzione o l'applicazione del teorema del confronto, o della regola di L'Hôpital per forme indeterminate.

Importanza dei limiti nel calcolo

I limiti sono alla base del calcolo differenziale e integrale. Due applicazioni chiave includono:

• Derivate: la derivata di una funzione in un punto è definita come il limite del rapporto incrementale della funzione in quel punto. Ciò fornisce una misura della rapidità con cui cambia il valore della funzione rispetto a un cambiamento dell'input.

• Integrali: l'integrale definito è formulato come il limite di una somma di Riemann, fornendo l'area sotto la curva di una funzione tra due punti.

I limiti non sono solo un concetto astratto, ma un elemento essenziale per l'analisi matematica e per la comprensione del mondo che ci circonda. Dall'ingegneria alla fisica, dalla biologia all'economia, l'abilità di modellare e comprendere il comportamento asintotico delle funzioni attraverso i limiti è indispensabile per il progresso scientifico e tecnologico. Con la loro capacità di descrivere il comportamento locale delle funzioni e di gestire situazioni complesse e forme indeterminate, i limiti rimangono uno dei concetti più potenti e versatili della matematica.