Limite infinito per x che tende ad un valore infinito
Nel vasto campo dell'analisi matematica, i limiti rappresentano uno dei concetti più interessanti e fondamentali. Particolarmente affascinante è il caso dei limiti infiniti per x che tende a un valore infinito. Questo scenario esplora il comportamento delle funzioni quando la variabile indipendente, x, cresce senza sosta verso l'infinito, sia positivamente (\(x \rightarrow +\infty\)) che negativamente (\(x \rightarrow -\infty\)). Questo tipo di limite rivela come una funzione risponde all'allontanamento indefinito da un punto di origine lungo l'asse delle x.
Definizione e contesto
Il concetto di limite infinito per x che tende all'infinito si occupa di situazioni in cui, man mano che x diventa arbitrariamente grande, il valore della funzione f(x) tende anch'esso a diventare infinitamente grande. Matematicamente, esprimiamo questo concetto come \(\lim_{x\to +\infty} f(x) = \infty\) o \(\lim_{x\to -\infty} f(x) = \infty\), a seconda della direzione verso l'infinito che consideriamo.
Definizione formale di limite infinito per x che tende all’infinito (positivo)
Si dice che \(\lim_{x\to +\infty} f(x) = \infty\) se, per ogni numero reale M > 0, esiste un numero reale N > 0 tale che per ogni x > N, si ha f(x) > M. In altre parole, man mano che x cresce senza limiti (diventa più grande di qualsiasi valore prefissato N), il valore della funzione f(x) supera ogni soglia M che abbiamo fissato, diventando così infinitamente grande.
Definizione formale di limite infinito per x che tende all’infinito (negativo)
Analogamente, Si dice che \(\lim_{x\to -\infty} f(x) = \infty\) se, per ogni numero reale M > 0, esiste un numero reale N < 0 tale che per ogni x < N, si ha f(x) > M. Questo significa che mentre x diventa arbitrariamente piccolo (andando verso valori negativi infiniti), il valore di f(x) continua a crescere oltre ogni limite M prefissato, tendendo all'infinito.
Interpretazione delle definizioni formali
Questa definizione formalizza l'idea che, indipendentemente da quanto grande (o piccolo, nel caso di \(-\infty\)) diventi x, esiste sempre un punto oltre il quale i valori di f(x) diventano maggiori di qualsiasi valore M che scegliamo. Ciò illustra un comportamento di crescita illimitata della funzione quando x si allontana indefinitamente dallo zero lungo l'asse dei numeri reali.
Calcolo dei Limiti Infiniti per x che Tende all'Infinito
Il calcolo di questi limiti richiede una comprensione profonda delle proprietà delle funzioni in gioco. Tecniche comuni includono la semplificazione algebrica, l'utilizzo di importanti teoremi sui limiti, e, in alcuni casi, l'applicazione di regole specifiche come la regola di L'Hôpital, che può essere particolarmente utile in situazioni di forme indeterminate.
Esempio di limite infinito per x che tende all’infinito
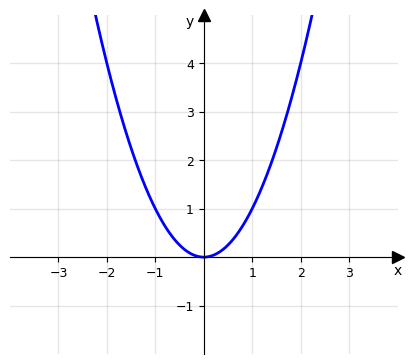
Consideriamo la funzione \(f(x)=x^2\). Intuitivamente, è evidente che man mano che x cresce senza limiti, anche f(x) diventa infinitamente grande. Matematicamente, esprimiamo questo concetto come \(\lim_{x\to +\infty} x^2 = \infty\). Un esempio più complesso potrebbe coinvolgere funzioni razionali, esponenziali o logaritmiche, dove il comportamento asintotico diventa meno immediato e richiede un'analisi più dettagliata.