Uguaglianza tra insiemi

Definito un insieme come una raccolta di elementi accomunati da una proprietà comune o semplicemente espressi tramite elencazione, esplicitiamo la condizione di uguaglianza tra due insiemi A, B come segue:

A = B ⇔  ( x ∈ A ⋀ x ∈ B )

cioè dato un elemento che appartenga all’insieme A si ha di conseguenza che esso appartiene anche all’insieme B e, viceversa, dato un elemento che appartiene B segue che esso deve appartenere anche ad A. 

Nota: Basta un solo elemento che non rispetti la precedente doppia implicazione per rendere i due insiemi diversi come mostrato nel seguente diagramma di Venn.

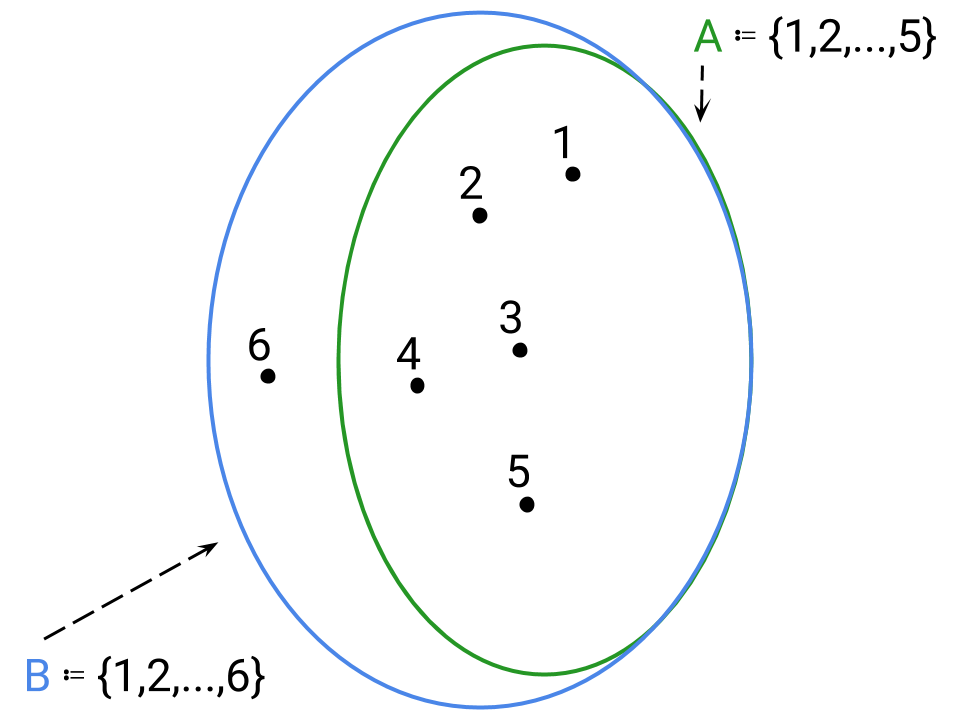
Una definizione equivalente della condizione di uguaglianza tra gli insiemi prevede l’utilizzo del concetto di sottoinsieme: si dice che un insieme A è sottoinsieme di un insieme B, o contenuto in B, se ogni elemento dell’insieme A appartiene anche all’insieme B; in notazione si scriverà A ⊆ B che equivale alla seguente espressione:

se ∀ x | x ∈ A ⇒ x ∈ B allora  A ⊆ B

Esempio 1: Il precedente diagramma di Venn usato per mostrare la non uguaglianza tra due insiemi è un caso particolare in cui l’insieme A ≔ {1, 2, 3, 4, 5} è contenuto in B ≔ {1, 2, 3, 4, 5, 6}.

Dato il concetto di sottoinsieme ne deriva un altro modo per descrivere l’uguaglianza tra due insiemi A, B generici che è quello della doppia inclusione:

A = B ⇔ ( A ⊇ B ⋀ B ⊆ A )

cioè i due insiemi A, B sono uguali se e solo se il primo insieme è contenuto nel secondo e il secondo nel primo: intuitivamente ciò ne decreta l’uguaglianza.

Cenno di dimostrazione:

(⇒) Siano A, B due insiemi e A = B; di conseguenza è banale che ∀ a ∈ A, a ∈ B ⇒ A ⊆ B e viceversa ∀ b ∈ B, b ∈ A ⇒ B ⊆ A.

(⇐) Sia A, B due insiemi generici con A ⊆ B ⋀ B ⊆ A. Supponiamo, per assurdo, che A ≠ B ovvero ∃ a ∈ A | a ∉ B ma questo contraddice l’ipotesi A ⊆ B secondo cui ∀ a ∈ A, a ∈ B. Analoga è la contraddizione dell’ipotesi di B ⊆ A nella supposizione di almeno un elemento b ∈ B che non appartenga ad A. La supposizione A ≠ B è dunque contraddittoria con le ipotesi di inclusione e se ne deduce che A = B necessariamente.