Le principali operazioni degli insiemi

Avendo ben chiaro il concetto di insieme e sfruttando i diagrammi di Venn per visualizzare meglio le operazioni svolte, procediamo elencando le principali operazioni insiemistiche con cui, dati A e B due insiemi generici, si ottiene un nuovo insieme risultante:

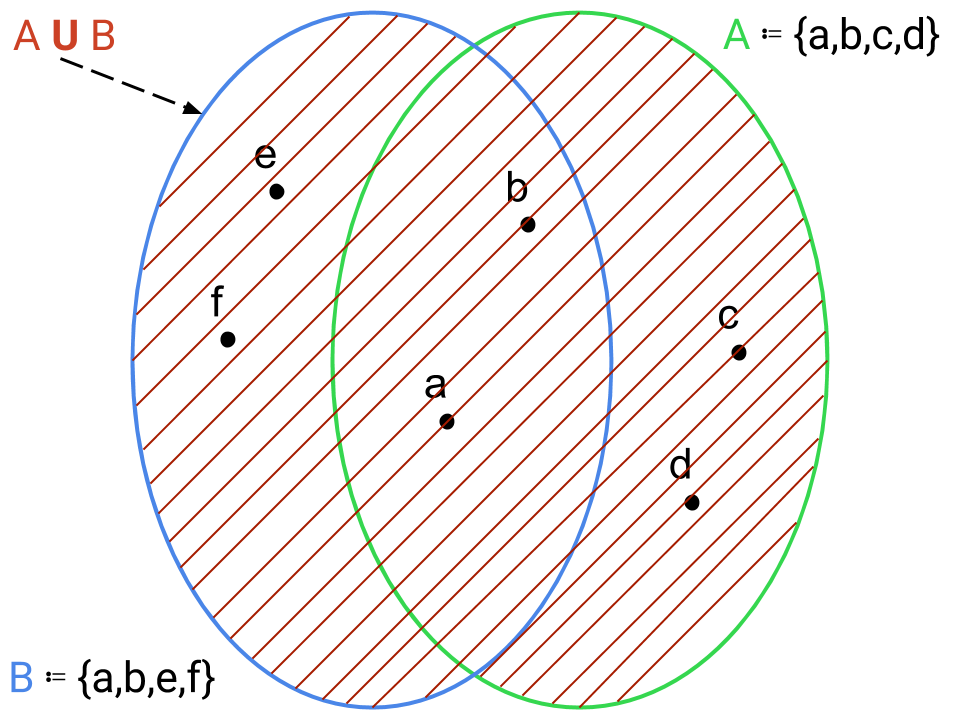
• unione di A e B: 

  A U B ≔ {x | x ∈ A ⋁ x ∈ B}

  ovvero è l’insieme costituito dagli elementi che appartengono almeno a uno dei due insiemi. Gli elementi dell’insieme unione possono anche appartenere ad entrambi poiché il simbolo logico V non implica la negazione.

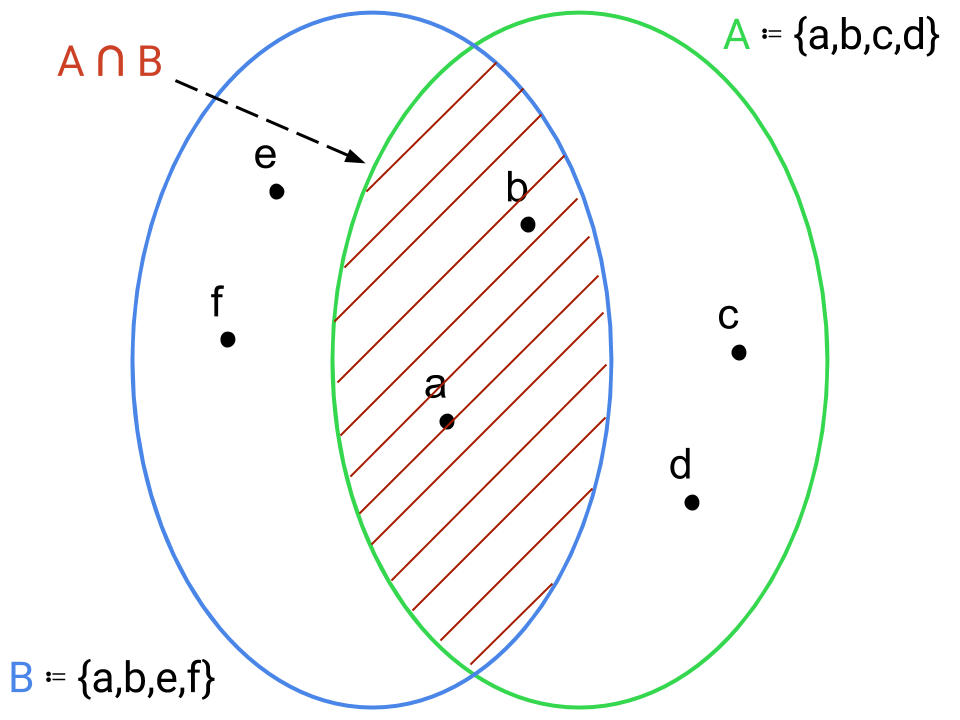
• intersezione di A e B: 

  A ∩ B ≔ {x | x ∈ A ⋀ x ∈ B}

  ossia l’insieme risultante comprende tutti gli elementi che appartengono simultaneamente ad entrambi gli insiemi di partenza; se A ∩ B = ∅ abbiamo due insiemi disgiunti, cioè che non hanno alcun oggetto in comune.

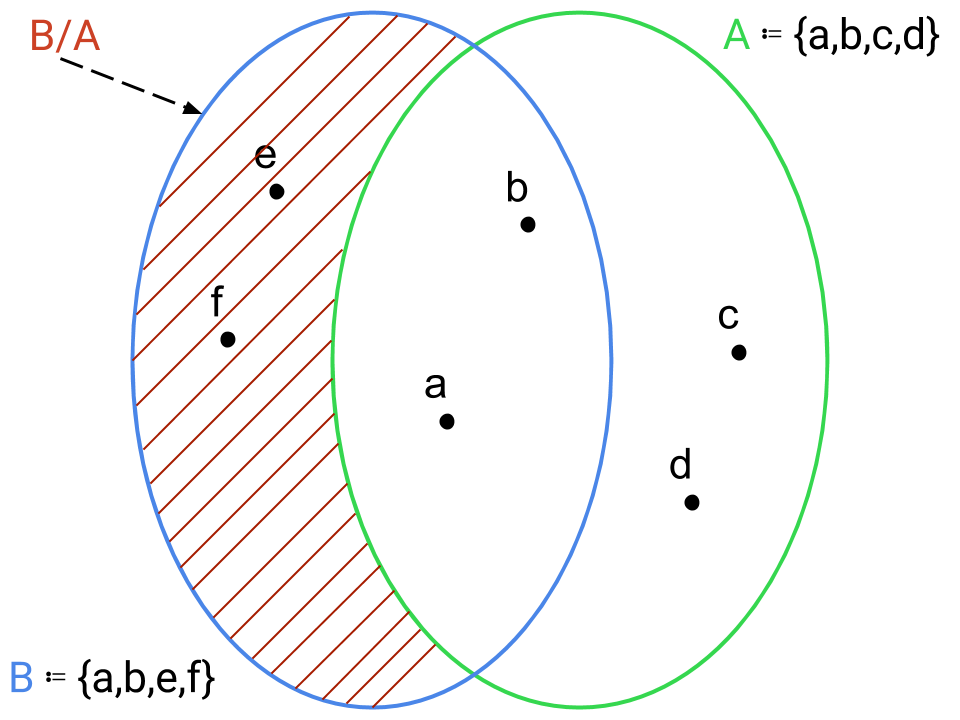
• differenza di A da B:

  B\A ≔ {x | x ∈ B ⋀ x ∉ A}

  è la classe di tutti gli oggetti del primo insieme (B) che contemporaneamente non appartengono al secondo insieme (A).

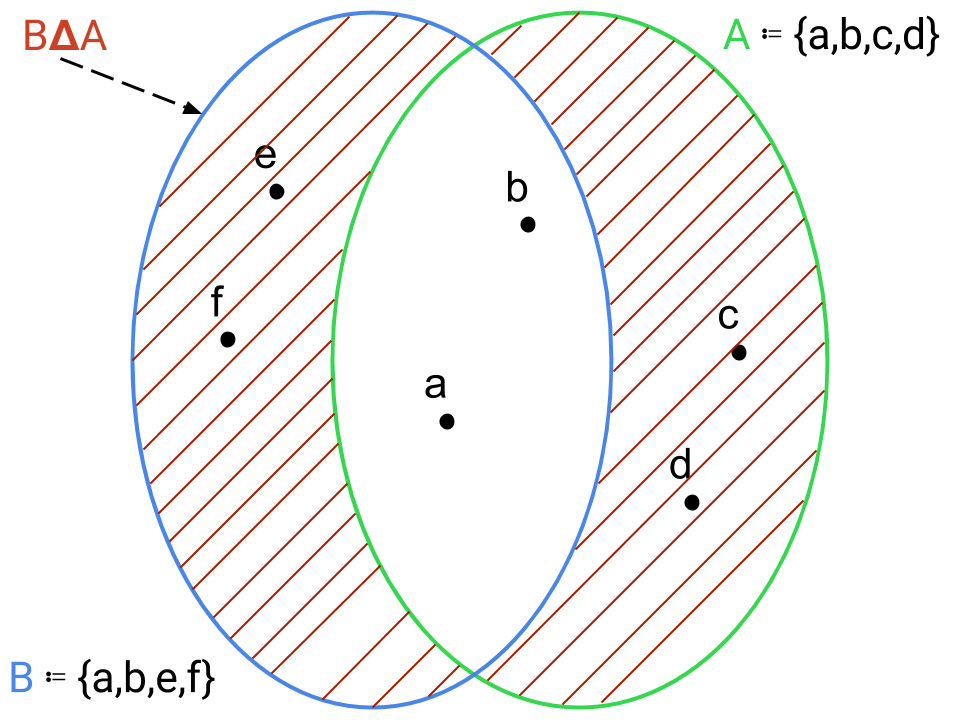
• differenza simmetrica di A e B:

  AΔB ≔ {x | (x ∈ B ⋀ x ∉ A) ⋀ (x ∈ A ⋀ x ∉ B)}

  che è l’unione dell’insieme degli elementi del primo insieme (A) che non appartengono al secondo (B), e degli elementi del secondo che non appartengono al primo. Un altro modo per descriverla è come l’unione dei due insiemi A e B a cui viene sottratta l’intersezione dei due, cioè gli elementi che appartengono ad entrambi gli insiemi.

AΔB = (A\B) U (B\A)

• complementazione: sia U un insieme detto insieme universo e sia la classe di tutti i sottoinsiemi propri e impropri di U l’insieme delle parti ℘(U) . Dato un insieme A ∈ ℘(U), è definito come complementare di A rispetto a U (𝓒 A) l’insieme U \ A:

𝓒 A ≔ {x : (x ∈ U) e (x ∉ A)}

𝓒 A ≔ U \ A

Tabella con le principali proprietà delle operazioni degli insiemi

Proponiamo una tabella che riassume le principali proprietà delle operazioni di unione e di intersezione che sono le più comuni. Per approfondire invitiamo a consultare le specifiche pagine (i link si trovano sui nomi del precedente elenco).

Elenchiamo inoltre le proprietà dell’operazione di complementazione; anche queste nozioni sono approfondibili attraverso le specifiche pagine, in particolare le leggi di De Morgan utili nell’esecuzione di operazioni tra insiemi.