Insieme universo: definizione ed esempi

Dato un insieme numerico A qualsiasi si vogliono elencare i suoi elementi tramite una notazione intensiva: è importante prestare attenzione all’insieme numerico di partenza da cui provengono questi elementi ed è qui che si rende necessario il concetto di insieme universo.

L’insieme universo, o insieme ambiente, è infatti l’insieme di partenza da cui vengono presi gli elementi che soddisfano le condizioni specificate con la notazione intensiva: ne consegue che tutti gli insiemi i cui elementi provengono da un dato insieme universo, indicato con U, siano sottoinsiemi dello stesso U.

Una definizione alternativa descrive l’insieme universo U come l’ambiente all’interno del quale possono essere definiti altri insiemi e questi, intuitivamente, saranno sottoinsiemi di U.

Nota: nella definizione e negli esempi che seguiranno sono stati usati insiemi numerici ma il concetto di insieme universo può essere utile nel caso di altri enti matematici (es. i vettori).

La rappresentazione secondo il diagramma di Venn prevede solitamente di utilizzare un rettangolo per rappresentare U, ma ciò non è vincolante: 

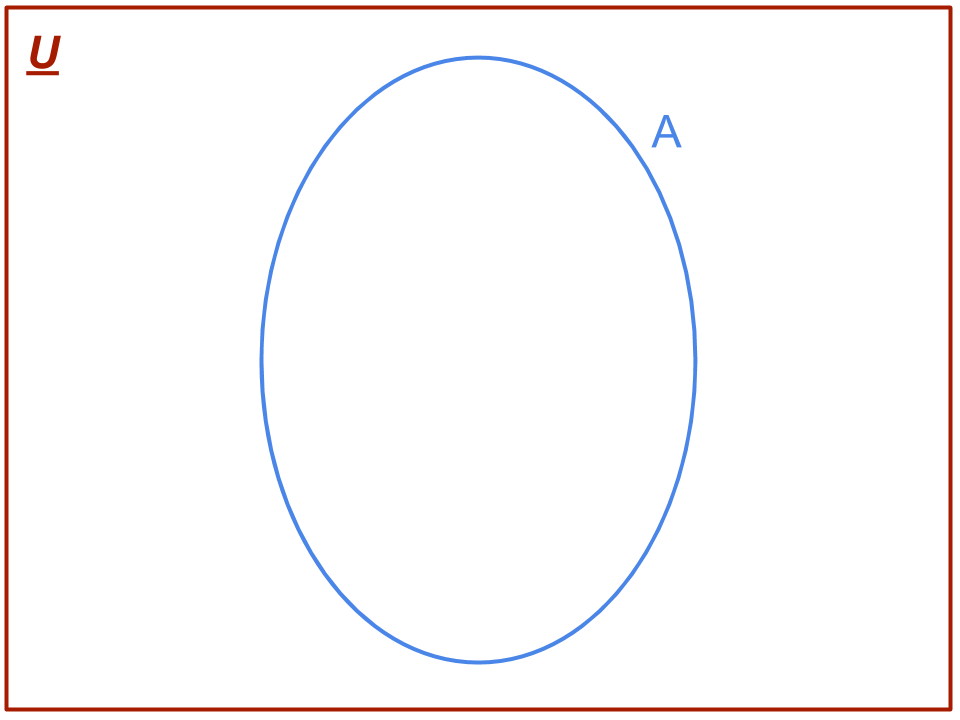
Esempio 1: Sia A ≔ {x | x ≤ 2}. Se non viene definito un insieme ambiente U dal quale vengono presi gli elementi si viene a creare una ambiguità nella definizione di insieme, dato che A potrebbe essere A ≔ {0, 1, 2} oppure A ≔ {2, 1, 0, -1, -2, ...} oppure ancora A ≔ {2, …, 3/2, …, 4/3, ...} e così via. Diventa perciò importante specificare l’insieme universo come segue:

A ≔ {x | x ∈ U  ⋀  "condizione"}

dove U può essere ℕ, ℤ, ℚ, eccetera mentre la “condizione”, nel nostro specifico esempio, coincide con x ≤ 2. Posto U ≔ ℕ come esempio si avrà:

Nota: dall’esempio 1 si può dedurre che l’insieme ambiente non è unico e non può essere dedotto a partire dall’insieme A generico; se U non è specificato, generalmente si assume come insieme di partenza quello dei numeri reali ℝ.