Verifica della suriettività di una funzione

Brevemente, una funzione f: X → Y si dice suriettiva se ogni elemento di Y ha almeno una controimmagine in X.

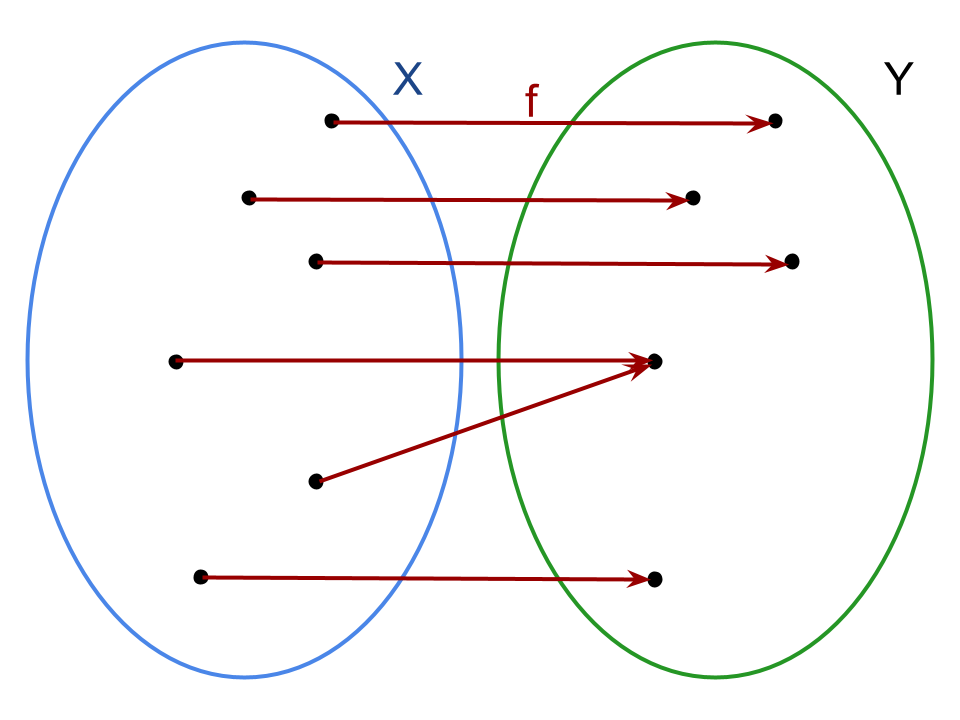
In linguaggio matematico diremo che un’applicazione f: X → Y è suriettiva se è verificato che 

∀y ∈ Y, ∃x ∈ X | f(x) = y

ovvero se ogni elemento di Y è immagine di almeno un elemento di X.

Nota: Se questa condizione è verificata insieme immagine, im(X), e codominio, cod(f), coincidono.

Come mostrato in funzioni suriettive, nel caso più comune di funzioni reali di variabile reale esiste un metodo grafico per verificare questa proprietà: si traccino delle rette orizzontali y = k, con k ∈ ℝ, e si verifichi che tutte queste rette intersecano almeno una volta il grafico della funzione.

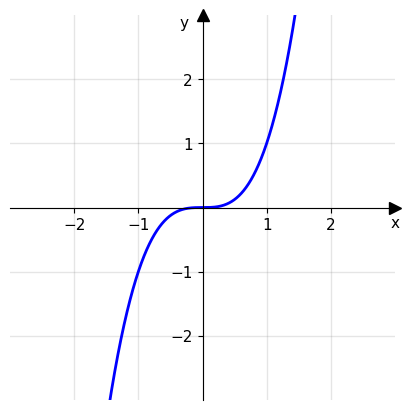
Tuttavia questo metodo richiede una non banale capacità di disegnare, almeno qualitativamente, il grafico di una funzione. Per questo motivo di seguito si illustra un metodo analitico che, nel caso di espressioni relativamente semplici, è altrettanto efficace nel verificare la suriettività o meno di una funzione.

Metodo analitico

Sia data una funzione, reale di variabile reale, y = f(x). Partendo dalla definizione di suriettività, cioè ∀y ∈ Y, ∃x ∈ X | f(x) = y, il procedimento da seguire è evidente:

• si considera la condizione y = f(x) come una equazione

• con le solite regole algebriche si risolve l’equazione esprimendo x in funzione di y

• si verifica che gli elementi x trovati appartengano al dominio della funzione

Sostanzialmente l’idea è quella di considerare un generico elemento y e verificare se esiste un generico elemento x, appartenente al dominio della funzione, che ne è la controimmagine. Se ciò è vero, per l’arbitrarietà della scelta di y, la funzione sarà suriettiva mentre, se ciò non è verificato, la funzione non lo sarà.

In alternativa, per dimostrare che una funzione non è suriettiva, basta trovare un solo elemento del codominio che non abbia controimmagine, cioè che non soddisfi l’equazione (anche se non è sempre così immediato individuarne uno).

Nota: Poiché la suriettività implica che insieme immagine e codominio coincidano, il problema è sostanzialmente quello di calcolare l’insieme immagine di una funzione e vedere se esso coincide col codominio.

Esempio 1: Si consideri la funzione polinomiale f: ℝ → ℝ definita dalla legge f(x) = 5x + 3 . Per verificarne la suriettività consideriamo l’equazione

y = 5x + 3

dove esprimiamo x in funzione di y con qualche passaggio algebrico:

y - 3 = 5x

\(x = \frac{y-3}{5}\)

e si osserva che ∀y ∈ ℝ, x è ben definita e appartiene al dominio ℝ: la funzione è quindi suriettiva.

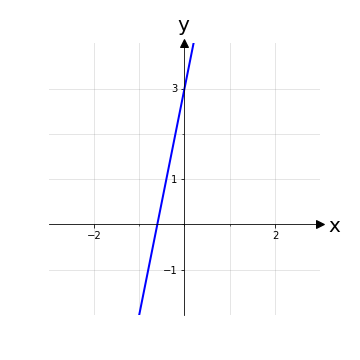
Esempio 2: Si consideri la funzione polinomiale f: ℝ⁺ → ℝ definita dalla legge f(x) = 5x + 3 . Per verificarne la suriettività i passaggi sono analoghi a quelli dell’esempio 1:

\(y = \frac{x-3}{5}\)

Tuttavia in questo caso, anche se ∀y ∈ ℝ l’espressione che lega x e y è ben definita, il dominio non è abbastanza per contenere tutte le controimmagini delle y: il dominio è definito come ℝ⁺≔ {x ∈ ℝ | x > 0} e, mettendo la condizione x > 0 a sistema con l’equazione di x in funzione di y si ottiene

\(x = \frac{y-3}{5}\) > 0

y - 3 > 0

y > 3

cioè il dominio ℝ⁺ contiene solo controimmagini per elementi y > 3. La funzione è chiaramente non suriettiva essendo il codominio ℝ. Per maggiore chiarezza si faccia riferimento al grafico dell’esempio 1 e si escludano mentalmente il secondo e terzo quadrante.

Controesempio: si prenda y = 0. Dalla relazione \(x = \frac{y-3}{5}\) risulta che la controimmagine debba essere x₀ = -35, tuttavia x₀ ∉ ℝ⁺.  

Esempio 3: Si consideri la funzione polinomiale f: ℝ⁺ → {y ∈ ℝ | y > 3} definita dalla legge f(x) = 5x + 3 . Per verificarne la suriettività i passaggi sono analoghi a quelli dell’esempio 1:

\(x = \frac{y-3}{5}\)

∀y ∈ ℝ l’espressione che lega x e y è ben definita ma, a differenza dell’esempio 2, il dominio è sufficiente per contenere tutte le controimmagini delle y e quindi la funzione è suriettiva.

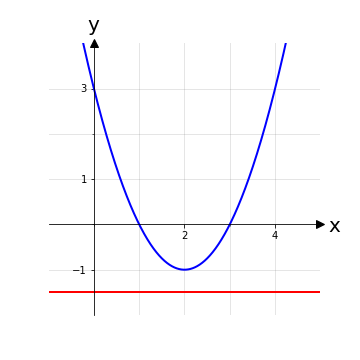
Esempio 4: Sia data la funzione polinomiale g: ℝ → ℝ definita dalla legge g(x) = x2-4x+3. Per verificarne la suriettività consideriamo l’equazione:

y=x2-4x+3

y-3=x2-4x

completando il quadrato:

y-3+4= x2-4x+4

y+1=(x-2)2

y+1=x-2

x = 2y+1

L’espressione trovata che lega x a y non è ben definita ovunque: ha soluzione solo per y+1 ≥ 0  ⇔  y ≥ -1. Tutti gli elementi dell’insieme {y ∈ ℝ | y < -1} non hanno controimmagine attraverso la funzione g, indipendentemente dalla scelta del dominio: la funzione quindi non è suriettiva.

Esempio 5: Sia data la funzione esponenziale h: ℝ → ℝ⁺ con legge h(x) = e2x. Per verificarne la suriettività consideriamo l’equazione

y = e^2x

e applichiamo il logaritmo naturale, operazione possibile dato che y > 0.

ln(y) = ln(e^2x)

ln(y) = x²

x = ± ln(y)

L’espressione trovata non è ben definita ovunque: ha soluzione solo per ln(y) ≥ 0  ⇔  y ≥ 1. Tutte gli elementi dell’insieme {y ∈ ℝ | 0 < y < 1} non hanno controimmagine attraverso la funzione g, indipendentemente dalla scelta del dominio: la funzione quindi non è suriettiva.

Nota: Da una funzione g: X → Y non suriettiva si può ottenere una funzione g’ suriettiva definendola come g’: X → im(X), x ⟼ g(x), ovvero semplicemente definendo una funzione con stesso dominio e legge ma con un codominio "comodo". Questa operazione è detta anche restrizione del codominio della funzione g.