Codominio di una funzione

Un discorso simile a quanto visto per il dominio di una funzione vale anche per il suo codominio.

Sia f una funzione definita come f: X → Y, x ⟼ f(x). Come visto nella definizione di una funzione, il codominio di f, cod(f), è l’insieme suggerito dalla definizione Y. Tendenzialmente, data una espressione analitica di una funzione, non viene specificato il suo dominio e codominio: di conseguenza, si assume per convenzione che il codominio naturale, o insieme di arrivo, di una funzione y = f(x) sia banalmente l’insieme ℝ.

Nota: La definizione di codominio usata in queste pagine non coincide con la definizione di insieme immagine di una funzione. Questa distinzione potrebbe venire meno in altri testi/fonti ma rimane sempre valido f(X) ⊆ Y, ovvero che l’insieme immagine è sottoinsieme, proprio o improprio, del codominio.

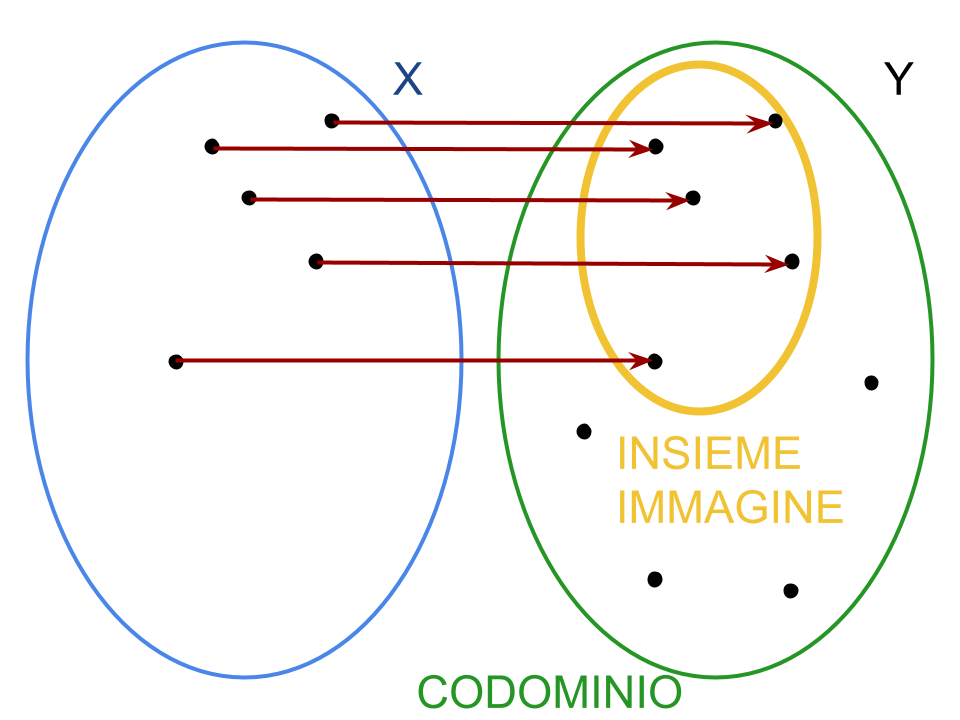
In particolare si noti come non tutti gli elementi del codominio abbiano un rispettivo elemento x nel dominio, mentre tutti gli elementi dell’insieme immagine sì: tali elementi del dominio sono dette controimmagini e l’insieme di tutte le controimmagini del codominio è, per definizione, il dominio stesso della funzione.

Esempio 1: Siano date le seguenti espressioni analitiche:

f(x) = x² - 3

g(x) = sin(x)

In assenza della definizione completa delle funzioni f e g, il codominio di entrambe sarà banalmente l’insieme ℝ, per convenzione.

Esempio 2: Siano date le seguenti funzioni:

f: ℝ → (0,+∞), x ⟼2x

g: (0,+∞) → ℝ, x ⟼x 

h: (0,+∞) → (0,+∞), x ⟼x

Come esplicitano le definizioni, i codomini per le funzioni f, g, h sono rispettivamente l’insieme (0,+∞), ℝ e (0,+∞) a prescindere dall’espressione analitica data.
Nota: A differenza dell’insieme immagine che va calcolato, il codominio o è dato nella definizione della funzione oppure è posto come ℝ per convenzione. In particolare se insieme immagine e codominio coincidono, f(X) = cod(f), allora la funzione f è detta suriettiva.