Insieme limitato, limitato superiormente o inferiormente

Avendo chiaro il concetto di ordinamento, sia X un insieme ordinato e A ⊆ X con A insieme non vuoto. A avrà un ordinamento indotto da X e sarà a sua volta ordinato.

Maggiorante e insieme limitato superiormente

Dato k ∈ X è detto maggiorante di A se soddisfa entrambe le seguenti condizioni:

1. k è confrontabile con ogni x ∈ A;

2. ∀ x | x ∈ A ⇒ x ≤ k ovvero qualsiasi elemento di A non è maggiore di k.

Se ∃ k ∈ X con queste proprietà, A viene detto insieme limitato superiormente.

Minorante e insieme limitato inferiormente

Analogamente dato t ∈ X è detto minorante di A se:

1. t è confrontabile con ogni x ∈ A;

2. ∀ x | x ∈ A ⇒ x ≥ t ovvero qualsiasi elemento di A non è inferiore a t.

Se ∃ t ∈ X con queste proprietà, A viene detto insieme limitato inferiormente.

Nota: Sia il maggiorante che il minorante non sono necessariamente unici.

Insieme limitato

Se entrambe le condizioni sono verificate, ovvero ∃ t, k ∈ X con le proprietà sopra definite, A è detto semplicemente insieme limitato.

Dato A ⊆ X non vuoto una definizione equivalente è la seguente:

• A si dice limitato superiormente se ∃ k ∈ X (detto maggiorante) | x ≤ k, ∀ x ∈ A

• A si dice limitato inferiormente se ∃ t ∈ X (detto minorante) | x ≥ t, ∀ x ∈ A

Nota: k ∈ X, maggiorante di A non deve necessariamente appartenere ad A stesso e, anzi, si può dimostrare come l’insieme A possa contenere al massimo un solo elemento che sia suo maggiorante: se esistono altri maggioranti essi non apparterranno sicuramente ad A. Un discorso analogo vale per il minorante.

Esempi di insiemi limitati superiormente e inferiormente

Esempio 1: X ≔ ℝ, A ≔ [-3, 1) ed evidentemente A ⊆ X.

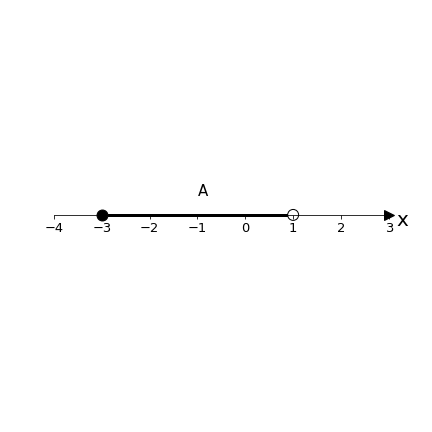
Ogni k ∈ [1,+∞) è un maggiorante e ogni t ∈ (-∞ , -3] è un minorante di A: l’insieme A si dirà limitato. Importante è notare come in questo caso tra i minoranti uno appartiene all’insieme stesso, -3, mentre tra i maggioranti nessuno appartiene all’insieme A. Avendo chiaro quanto specificato nella Nota ciò non dovrebbe sorprendere. 

Esempio 2: Y ≔ ℝ, B ≔ (2, +∞) ed evidentemente B ⊆ Y.

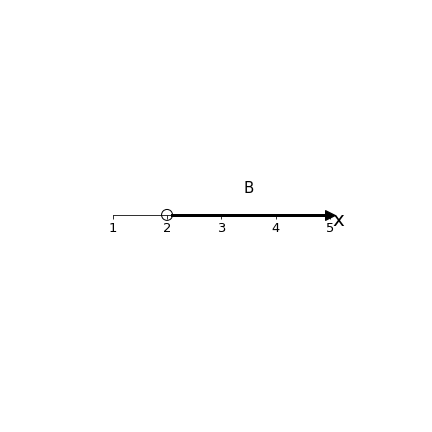
Ogni t ∈ (-∞ , 2] è un minorante di B; tuttavia non è possibile trovare un elemento di B che lo limiti superiormente, ovvero ∄ k | ∀ y ∈ B, k ≥ y. L’insieme B si dirà inferiormente limitato.
Nota: Si noti che possono esistere più maggioranti e minoranti di un insieme ma ne basta trovare uno per poterlo definire limitato superiormente o inferiormente.